Introduction to C Language
Programming – To solve a computing problem, its solution must be specified in terms of sequence of computational steps such that they are effectively solved by a human agent or by a digital computer.
Computer Program – A program is a set of logically related instructions that is arranged in a sequence that directs the computer in solving a problem. The Process of writing a program is called programming.
Software – Software is a collection of computer programs and related data that provides the instructions for telling a computer what to do and how to do it. Software classification can be given as-
1. Application Software : Application Software directs computers to resolve the user’s problems such as finance related Software, Airline, Railway Reservation software, Ms-Office, Ms-paint, etc.
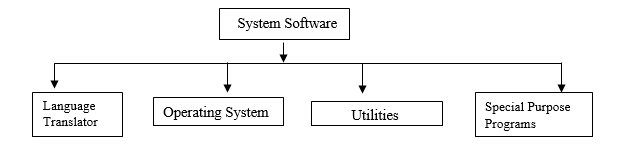
2. System Software : System Software is a collection of programs that interface with the hardware. Most significant system software is the Operating system
Operating System – It is the interface between the computer hardware and the user for communication purposes. DOS, Windows, Linux, Unix etc, are different examples of operating systems
Number System –
1. Decimal number System: It consists of 10 symbols (0 to 9) Therefore, the base of the system is 10.
2. Binary Number System : It consists of a total 2 symbols (0,1) Therefore, the base of the system is 2.
3. Octal Number System : It consists of 8 symbols (0 to 7) Therefore, the base of the system is 8.
4. Hexadecimal Number System: It consists of 16 symbols (0 to 9 and A, B, C, D, E, F). Therefore the base of the system is 16.Language –
1. Natural Language: Human to Human Communication can be carried out using natural languages such as English, Hindi, French and Japanese etc.
2. Programming Languages: A Program Communicates with the computer through a medium called programming language. Programming language can be classified into two groups:
‘C’ Language Character Set- The set of acceptable character for any language is called as its character set.
Keywords
The C keywords are reserved words by the compiler. All the C keywords have been assigned fixed meaning The Keywords cannot be used as variable names because they have been assigned fix jobs. It is suggested not to mix up keywords with variable names. For using the keywords in the program, no header file is to be included.
Additional keywords for Borland c
Data Types in C
1. Integral type –
2. Floating point types
Note : ‘C’ languages are a case sensitive languages. Entire programming must be done in lower case letters.
Variable – Variable is a name of memory location where we can store any data. It can store only single data (latest data) at a time. In C, a variable must be declared it can be used. Variables can be declared at the start of any block of code, but most are found at the start of each function.
Rules for declaring the variable names:
1. A variable name is a combination of alphabets, digits or underscores. Do not write unnecessary long names as it adds to your typing effort.
2. The first character in a variable name should be an alphabet or underscore.
3. No commas or blanks are allowed in the variable name.
4. No special symbols other than underscores are allowed in a variable name.
5. Try giving some relevant variable names.
6. Variable name must be other than keywords.
7. It is advisable to use small case letters for variable name. Example of valid variable names are shown below
X result radius volume x1 x2 num power length n
DECLARATIONS – All variables must be declared before they can appear in executable statements. A declaration specifies a data type and contains one or more variables of that type.
Single variable declaration
Syntax:
Datatype variablename:
Ex. float r;
Multiple variable declaration.
Syntax:
Datatype Variablename 1, Variablename 2…………. Variablename n:
Ex. int a, b, c
Float x1, x2;
Where a, b, and c are declared to be integer variables, x1 and x2 are floating- point variables.
float x1; /*root 1 of quadratic equation */
float x2; /*root 2 of quadratic equation */
Last two declarations takes more space, but it is convenient for adding comments explaining their purpose to Each declaration.
Assigning the value at the time of declaration is called as initialization. Variable can be initialized in following ways.
int x =2;
In the above statement declaration and initialization of variable is done in the same statement.
int x;
x =2;
In the above statement in the first line integer variable x is declared and second statement it is initialized with value 2.
int x,y,z
x=y=z=3;
In the above statement in the first statement three variables x, y and z are declared. In the second statement they are initialized with value 3
Consider the declaration
int i =3
This declaration tells the C compiler to :
(a) Reserve space in memory to hold the integer value.
(b) Associate the name i with this memory location.
(c) Store the value 3 at this location.
We may represent i' s location in memory by the following memory map
We see that the computer has selected memory location 65524 as the place to store the value 3. The location number 65524 is not a number to be relied upon, because some other time the computer may choose a different location for storing the value 3. The important point is, i’s address in memory is a number.
What is difference between variable and constant?
A variable is a data name used to store values of different data types. The constants in C are applicable to the value, which do not change during program execution.
DIFFERENT TYPES OF CONSTANTS IN C
The Constants in C are applicable to the values, which do not change execution of a program. There are several types of constants in ‘C’ They are classified into following types.
A) Numerical Constants
1) Integer Constants: These are the sequence of numbers from 0 to 9 without decimal points or fractional part of any other symbols. It requires minimum two bytes and maximum four bytes. Integer constant could be either positive or negative or may be zero. The number without a sign is assumed as positive
Example: 10, 20, +30, -15 etc.
2) Real Constants: Real constants are often known as floating point constants Integer constants are unfit to represent many quantities, Many parameters of quantities are defined not only in integers but also in teal numbers. For example length, height, prize, distance etc. are measured in real numbers
Examples: 2.5, 5.521, 3.14 etc.
The real constants can be written in exponential notation, which contains fractional part and exponential part For example, the value 2456 123 can be written as 2.4561 X e+3
The general format of the real number contains mantissa and exponent. The mantissa is either a real number represented in decimal or an integer The exponent is an integer number may be positive or negative. The lettere separating the mantissa and exponent can be written in lower or upper case
B) Character Constant
1) Single Character Constants: A character constant is a single character. They are also represented with single digit or a single special symbol or white space enclosed with in pair of single quote marks.
Example: a', '8", ‘!’ etc
Character constants have integer values known as ASCII values. For example the statement
printf ("%c %d", 65, 'B') will display character A and 66.
2) String Constants: String constants are sequence of characters enclosed with in double quote marks. The string may be combination of all kinds of symbols
Examples "Hello, “India”, “444”, “a”,
Operators in C
1. Arithmetic operators ( +, -, *, /, %)
Module in the operation that gives the remainder of a division of two integer values. For example, if we write a-11% 3; the variable a will contain 2 as the result since 2 is the remainder from dividing 11 between 3
2. Assignation (=):
The Assignment Operator evaluates an expression on the right-hand side of the expression and substitutes it to the variable appears to the left of the expression Example: x = a + b
Here the value of a + b is evaluated and substituted to the variables. It is necessary to emphasize that the assignation operation always takes place from right to left and never at the inverse a=b.
3. Compound assignation operators (+=, -=, *=, /=, %=, >>=, <<=, &=, ^=, l=)
Value += increase; is equivalent to value = value + increase;
a-= 5; is equivalent to a=a-5;
a/=b; is equivalent to a =a/b;
price *=units + 1; is equivalent to price = price* (units + 1); and the same for all other operations
4. Unary increment and decrement: (++ /--): They increase or reduce the value of variable by 1.
a++; a+=1: a=a+1; All are equivalent in its functionality: value of a is incremented by 1.
a--; a+=1: a=a+1; All are equivalent in its functionality: value of a is decrement by 1.
5. Relational operators (==, !=, >, <, > =, <=)
In order to evaluate a comparison between two expressions we can use the Relational operators. As specified by the ANSI -C standard, the result of a relational operation in s bool value that can only be 1 (true) or 0 (false), according to the result of the program.
We may want to compare two expressions, for example, to low if they are equal or if one is greater than the other. Here is a list of the relational operators: Be aware. Operator = (one equal sign) is not the same as operator == (two equal signs), the first is an assignations operator (assigns the right side of the expression to the variable in the left) and the other (= =) is a relational operator of equality that compares whether both expressions in the two sides of the operator are quo each other.
6. Logic operators (!, &&, ||):
Operator! is equivalent a Boolean operation NOT and the only thing that it does is to invert the value of it. It returns the opposite result of evaluating in operand.
For example:
Logic operators && and || are used when evaluating two expressions to obtain a single result. They correspond with Boolean logic AND and OR respectively.
Truth Table
7. Ternary Operator – The ? (ternary condition) operator is a more efficient from for expressing simple if statements. It has the following form
expression l ? expression 2 : expression3
It simply states:
if expression1
then expression2
else
expression3
For example, to assign the maximum of a and b to z: z = (a>b)? a: b; which is the same as:
If (a>b)
z = a;
else
z = b;
7. sizeof () -The operator accepts one parameter that can be either a variable type or a variable itself and returns the size in bytes of that type or object: a = sizeof (char);
8. Bitwise Operators (&, l, ^, ~, <<, >>) – Bitwise operators modify variables considering the bit patterns that represent the value they store.
Definition of Bitwise logical operators:
Example:

OPERATOR PRECEDENCE AND ASSOCIATIVITY

Operator precedence describes the order in which c evaluates different operators in a complex expression. For example, in the expression a = 4+b*2, Which happens first, the addition or the multiplication? The operator precedence will tell us which operation should perform first. The operator which is having highest precedence will evaluate first and the operator which is having lowest precedence evaluate last. If two operators are on the same level of precedence, then the order they will be evaluated in is going to be considered. This is known as Associativity property of an operator.
PROGRAMMING METHODOLOGY
A computer is used to solve a problem.
Steps
1. Analyze the problem
2. Identify the variables involved
3. Design the solution.
4. Write the program
5. Enter it into a computer
6. Compile the program and correct errors
7. Correct the logical errors if any
8. Test the program with data
9. Document the program
DEFINING A PROBLEM STATEMENT –
Whenever we solve any problem, we must define the problem. Consider a situation where XYZ Company is low on sale. Then the problem for sales manager to define problem properly before the Owner thinks of solving the problem. If the sale is low because of place, then his problem is placing therefore solution is to change the place to increase the sale. If the problem of low sale is because of the lack of the demanded goods for the customer, then his job is to look after the production of the demanded goods etc.
Similarly, in computer programming i.e when making a program we should have well defined problem. Note in computer programming, the term problem is the task to be performed. This problem has to be defined precisely so as to ensure the proper solution. This is one of the very important aspects of the problem solving that the problem should be well defined.
The problem defining has to undergo a various stage. This is shown in following figure
Thus, the problem statement development begins from initially defining the problem. The problem statement once defined, and then the attempt should be made to solve the problem. You will come across many new things to be considered and implemented and hence you can redefine the problem statement accordingly. Thereafter scale the problem, for a larger data set and hence define the problem statement more precisely.
Thus, problem statement can be defined and redefined using the process as seen in above figure.
Once the problem is precisely defined then an algorithm is required to implement the same. The algorithm can then be implemented using a programming language. In the further part of this chapter, we will see what is an algorithm and to write the same. In the later chapters we will see the implementation of various algorithms using
The C programming language.
ALGORITHM AND FLOWCHART
In order to write computer programs without any logical error, it is recommended for programmers to prepare a rough writing showing the steps involved in the program. This is called an algorithm.
An algorithm presents step-by-step instructions required to solve any problem. These steps can be shown diagrammatically using a flowchart.
Algorithm
An algorithm is a finite set of statements, each of which has a clear meaning and be executed in a finite amount of time and with a finite amount of time. the process of the programming is shown as follows
An algorithm is an English language representation of the sequence of steps to be executed to perform a given task. An algorithm can be defined in simple terms as description of the steps necessary to solve a problem. The algorithm should define the procedure to perform the given task.
Graphical representation of an algorithm can be done using flowchart or pseudo code.
Properties of Algorithm – The algorithm should have the following properties associated with it:
a. Non- ambiguity: This property of an algorithm indicates that each of the statement in the algorithm must be clear and precise. There must be no ambiguity in any of the statement.
b. Range of input: The range of the input for which the algorithm works is also to be compulsorily mentioned in the algorithm. There should be clear indication for the range of inputs for which the algorithm may fail.
c. Multiplicity: The algorithm can be represented in multiple ways; an algorithm can be written in English language or by the graphical representation called as flowchart or the pseudo code.
d. Speed: The one of the important properties of an algorithm is that it should produce the result at a fast speed or efficiently.
e. Finiteness: The algorithm should be finite i.e. there should be no infinite condition leading to a never-ending procedure and hence never completing the task.
Developing an Algorithm
The algorithm creation is a logical task. It requires logic development and cannot be done automatically. It requires various considerations so as to develop an algorithm that is better and efficient.
Space Complexity (Efficiency)
It is very important that the algorithm implemented should be such that it requires less memory space. The space complexity can be defined as the memory space required for an algorithm to be executed. The space required in memory for an algorithm to be executed can be divided into two parts, viz constant (C) and instance (Sp). The constant space is required for storing the variables, program tec., The Instance space is required depending on the problem case or is input dependent. Thus, the space required S(p) for implementing an algorithm can be given as:
S(p) = C + Sp
The parameter C in the equation is a fixed term that depends on the variables required to be declared in the algorithm. This term also includes the space required to store the program or the instructions of the program used to implement the algorithm.
But some of the inputs are to be taken from user, and this input size may depend on users’ choice. For example, if there are ‘n’ number to be added, wherein the value of the ‘n’ is to be taken from user then the number of input values to be taken can be decided only during the execution. These variable size input requires memory space defined by the term Sp in the above equation.
Time Complexity (Efficiency)
The time complexity of an algorithm is the time required by the computer to execute the program implemented according to the corresponding algorithm. The calculation of time required to execute the program depends on various other parameters besides the algorithm implementation. The different parameters on which the execution time depends are instruction set used, other programs running in the computer, hardware or processor speed etc.
The time complexity is hence given in terms of frequency where the frequency is the number of times the instructions are to be executed. For example, if the instructions are to be executed for ‘n’ times (where ‘n’ is the input size or number of input values) then the time complexity is said to be ‘n’
We can have three cases to analyze time complexity of an algorithm-
1) Worst Case - O (Big Oh)
2) Average Case - Ω (Omega)
3) Best Case - Ɵ (theta)
Worst Case Analysis – It describes the maximum time taken by an algorithm. Big oh notation is used to describe worse case analysis of an algorithm.
In the worst-case analysis, we calculate upper bound on running time of an algorithm. We must know case that causes maximum number of operations to be executed. For Linear Search, the worst case happens when the element to be searched is not present in the array.
Best Case Analysis – It describes the minimum time taken by an algorithm. Theta notation is used to describe best case analysis of an algorithm. In the best-case analysis, we calculate lower bound on running time of an algorithm. We must know the case that causes minimum number of operations to be executed. In the linear search problem, the best case occurs when number to be searched is present at mid position of an array.
Average Case Analysis – It describes the average time taken by an algorithm. Omega notation is used to describe average case analysis of an algorithm
In average case analysis, we take all possible inputs and calculate computing time for all of the inputs.
Flowchart
Flowchart is a symbolic or diagrammatically representation of an algorithm. It uses several geometrical figures to represents the operations, and arrows to show the direction of flow. Following are the commonly used symbols in flowcharts.
Flow Chart Symbols
The following are some guidelines in flowcharting:
a) In drawing a proper flowchart, all necessary requirements should be listed out in logical order.
b) The flowchart should be clear, neat and easy to follow. There should not be any room for ambiguity in understanding the flowchart.
c) The usual direction of the flow of a procedure or system is from left to right or top to bottom.
d) Only one flow line should come out from a process symbol.
e) Only one flow line should enter a decision symbol, but two or three flow lines, one for each possible answer, should leave the decision symbol.
Only one flow line is used in conjunction with terminal symbol.
g) Write within standard symbols briefly. As necessary, you can use the annotation symbol to describe
data or computational steps more clearly.
h) If the flowchart becomes complex, it is better to use connector symbols to reduce the number of flow lines.
Avoid the intersection of flow lines if you want to make it more effective and better way of communication.
i) Ensure that the flowchart has a logical start and finish.
j) It is useful to test the validity of the flowchart by passing through it with a simple test data.
ADVANTAGES OF USING FLOWCHARTS
1. Communication: Flowcharts are better way of communicating the logic of a system to all concerned.
2. Effective analysis: With the help of flowchart, problem can be analyzed in more effective way
3. Proper documentation: Program flowcharts serve as a good program documentation, which is def various purposes.
4. Efficient Coding: The flowcharts act as a guide or blueprint during the systems analysis and development phase
5. Proper Debugging: The flowchart helps in debugging process.
6. Efficient Program Maintenance: The maintenance of operating program becomes easy with the help of flowchart. It helps the programmer to put efforts more efficiently on that part.
LIMITATIONS OF USING FLOWCHARTS
1. Complex logic Sometimes, the program logic is quite complicated. In that case, flowchart becomes complex and clumsy
2. Alterations and Modifications If alterations are required the flowchart may require re-drawing completely.
3. Reproduction: As the flowchart symbols cannot be typed, reproduction of flowchart becomes a problem.
4. The essentials of what is done can easily be lost in the technical details of how it is done.




























Post a Comment